[Coding023] Sort - 选择排序
堆排序
Ben
2024/01/07
Get the knowledge flowing and circulating! :)
目录
标题:堆排序
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。
堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
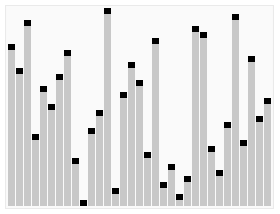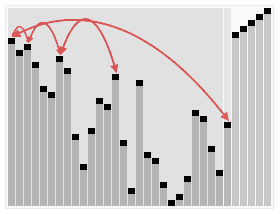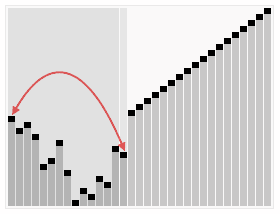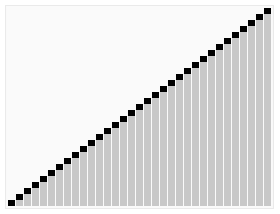
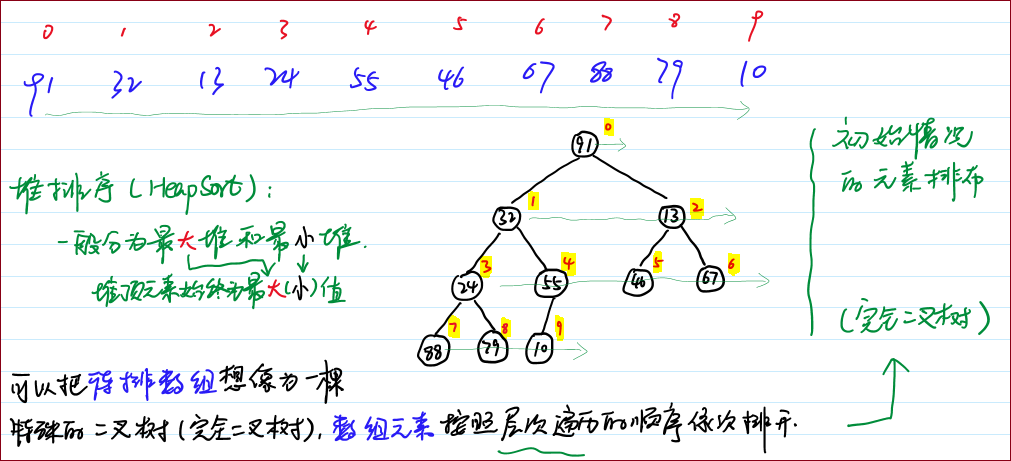
Fig. 堆排序算法的演示。
首先,将元素进行重排,以符合堆的条件。图中排序过程之前简单地绘出了堆树的结构。若以升序排序说明,把数组转换成最大堆(Max-Heap Heap)。
这是一种满足最大堆性质(Max-Heap Property)的二叉树:对于除了根之外的每个节点i, A[parent(i)] ≥ A[i]。
重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换,把交换后的最后一个结点移出堆),并让残余的堆维持最大堆性质。
堆节点的访问
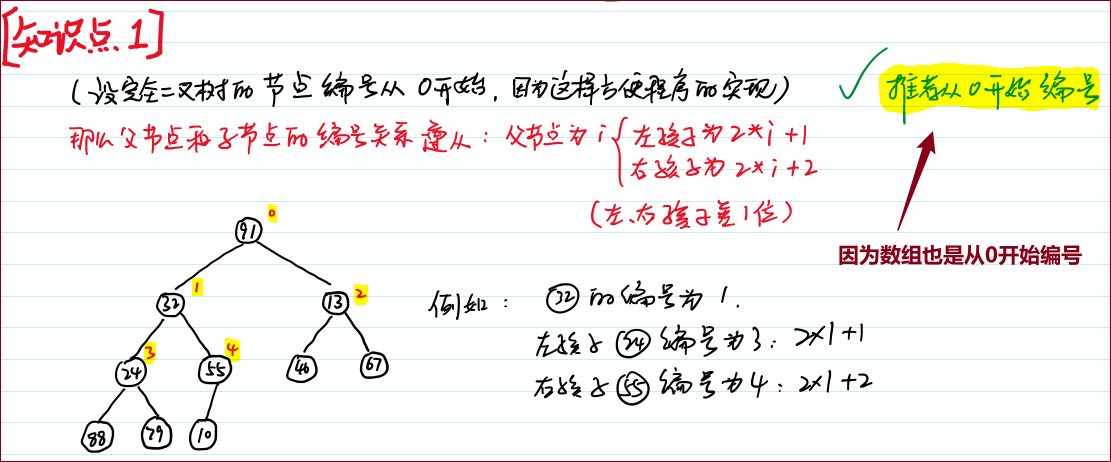
通常堆是通过一维数组来实现的。在数组起始位置为0的情形中:
父节点
的左子节点在位置 ; 父节点
的右子节点在位置 ; 子节点
的父节点在位置 ;
向上取整
- $\lceil x \rceil$向下取整
- $\lfloor x \rfloor$在堆的数据结构中,堆中的最大值总是位于根节点(在优先队列中使用堆的话堆中的最小值位于根节点)。堆中定义以下几种操作:
最大堆调整(Max Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
建立最大堆(Build Max Heap):将堆中的所有数据重新排序
堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
——维基百科
堆排序基础
涉及知识点

堆排序思想步骤解读(手绘示意图)
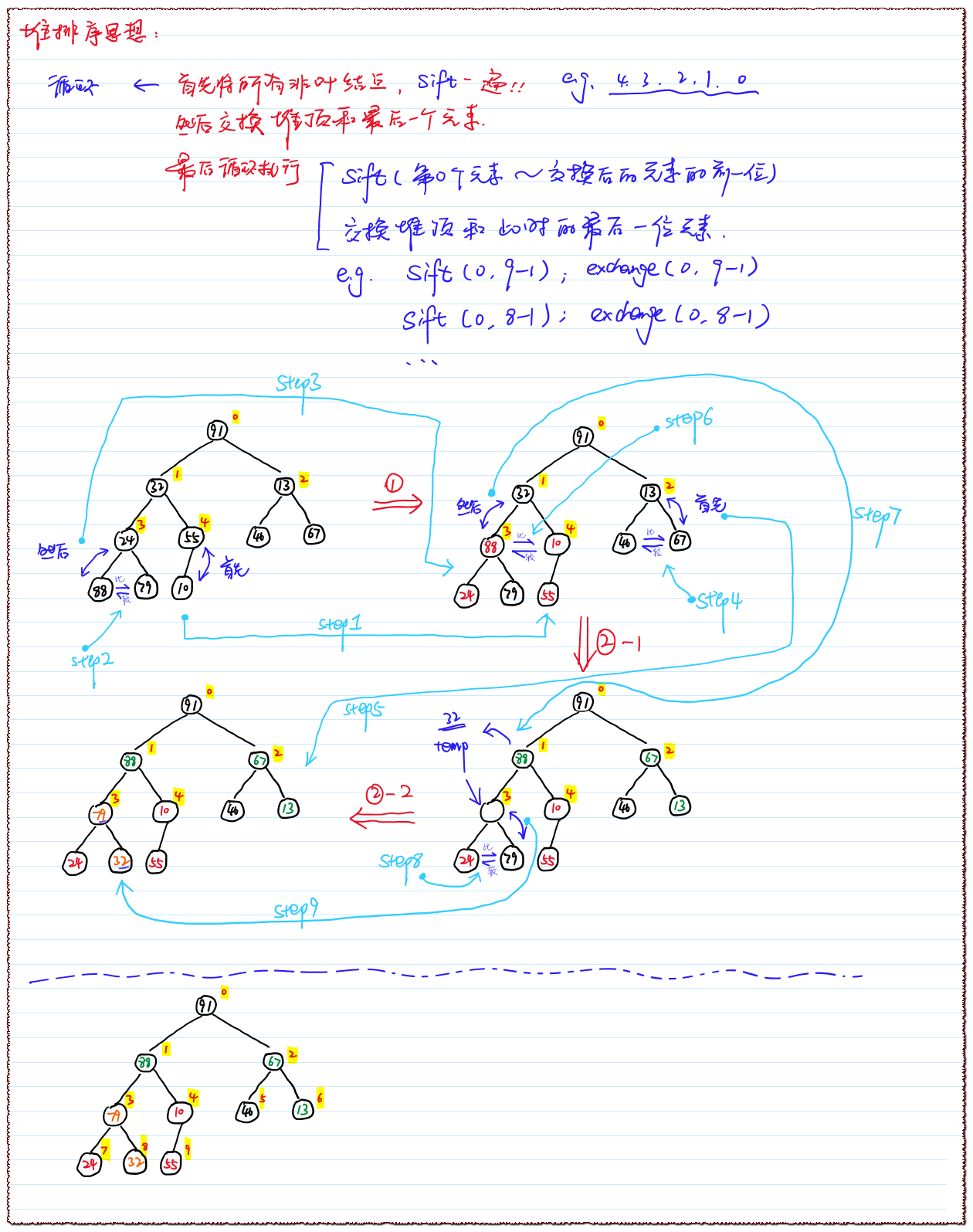
※ 一次完整的排序手绘图
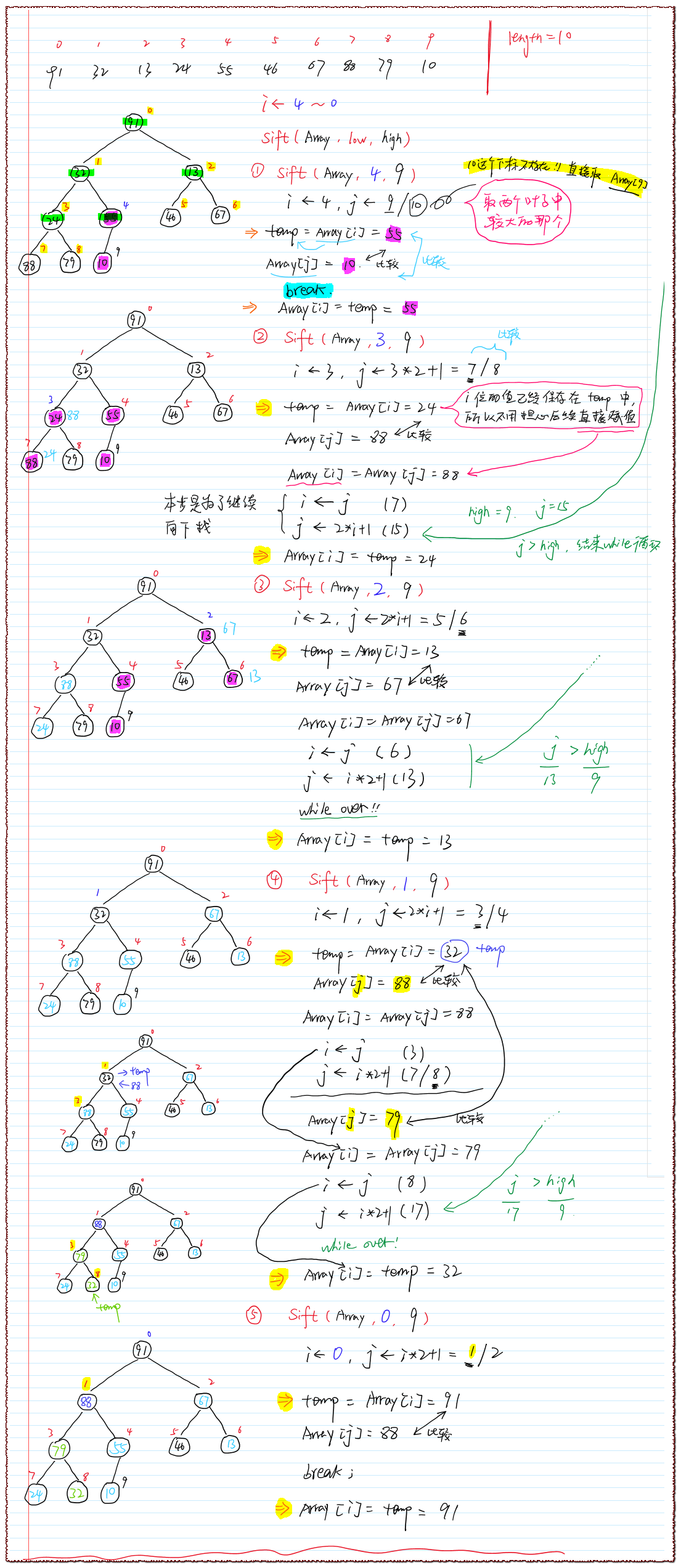
▲ 特殊情况注意(这种情况不会存在的!)
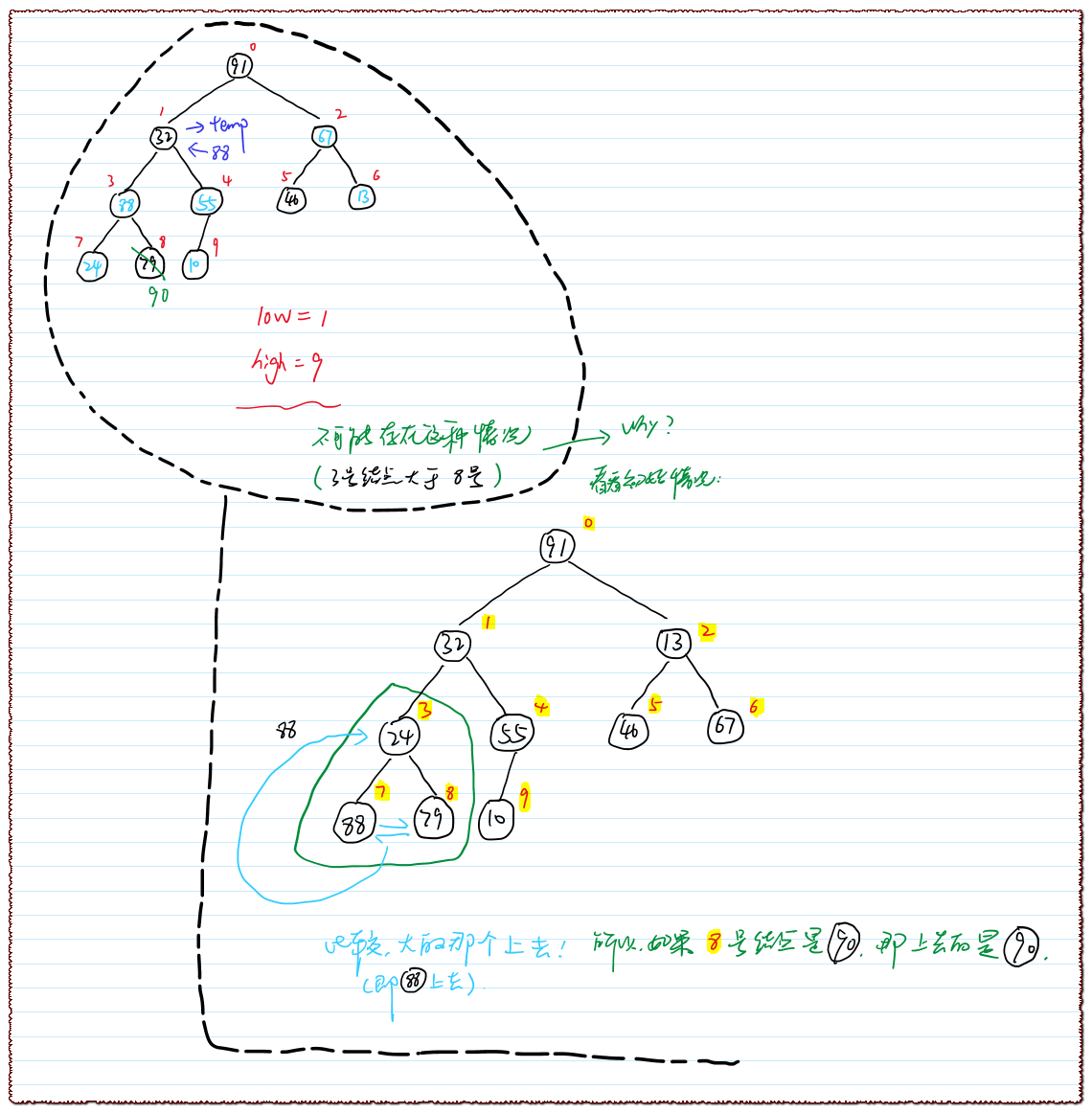
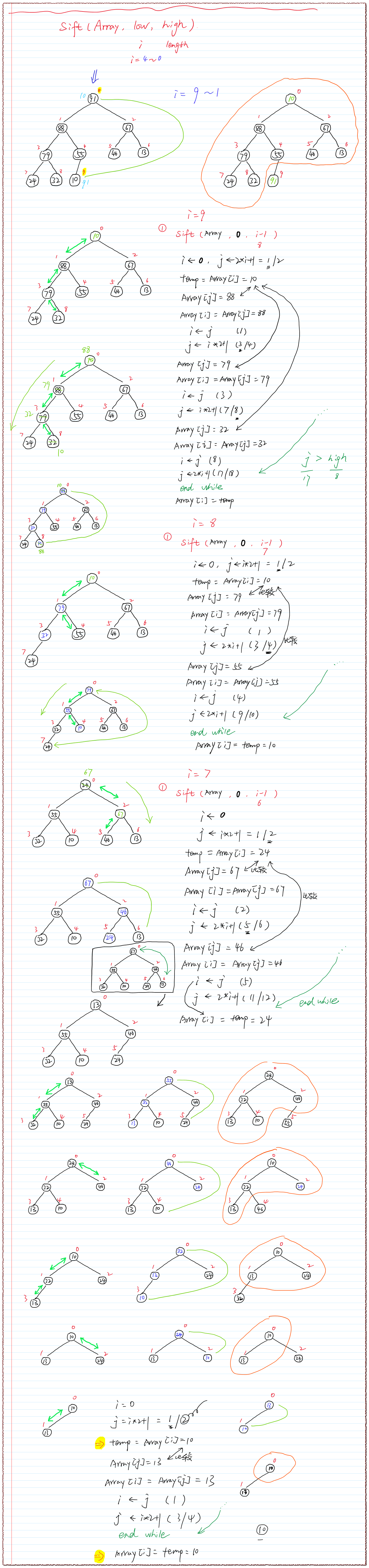
※ 另一个直观的例子
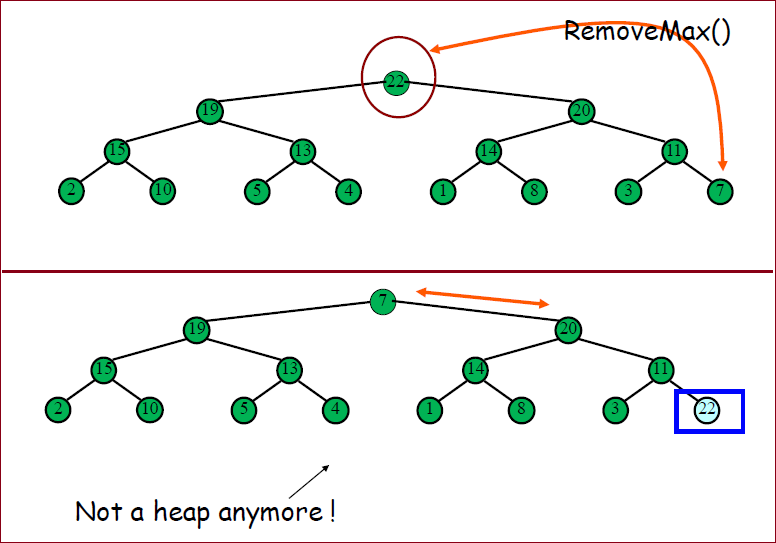
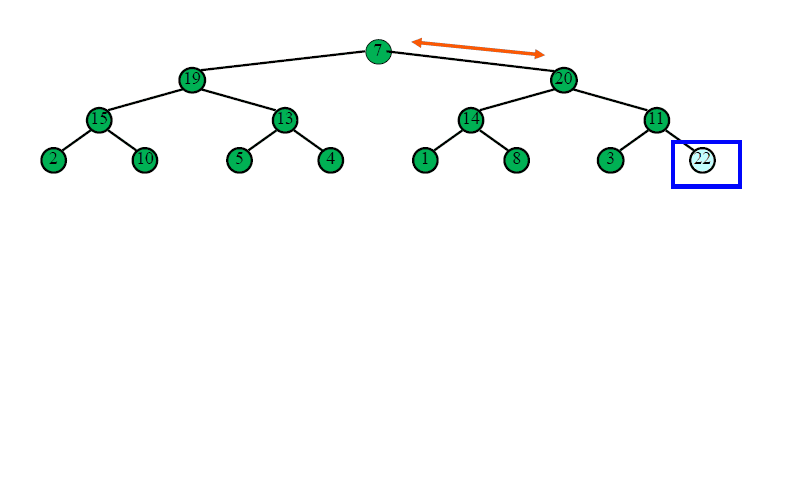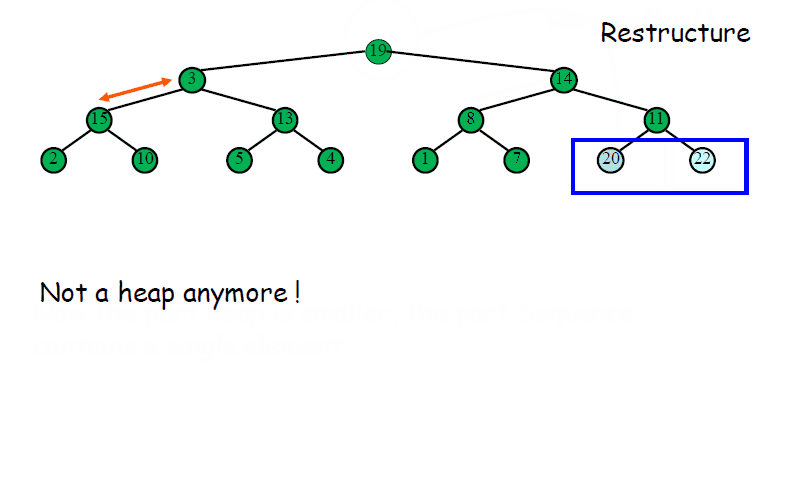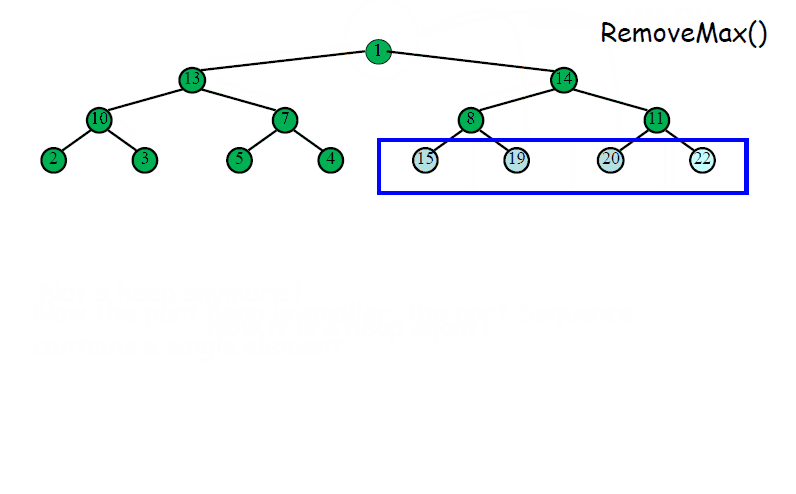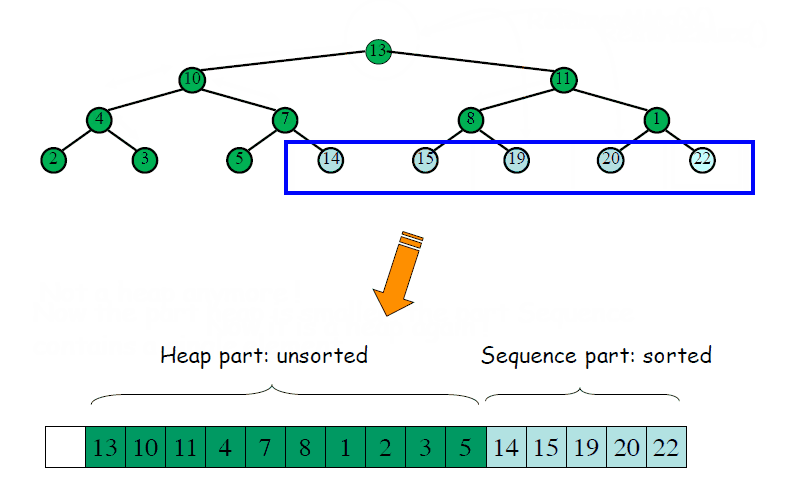
C语言代码实现
891
3void Sift(int* array, int low, int high) {4 5 int i = low;6 int j = i * 2 + 1;7
8 // 拿到父节点的数值9 int temp = array[i];10
11 while(j <= high) 12 {13 // 两个孩子节点,哪个更大一点,哪个和父节点 PK14 if(j < high && array[j] < array[j + 1]) 15 {16 j++;17 }18
19 // 孩子节点如果大于父节点,把孩子值给父节点,然后让孩子成为父节点,往下继续处理20 if(array[j] > temp) 21 {22 array[i] = array[j];23 i = j; // 继续往下处理 (新的父节点)24 j = i * 2 + 1; // 新的子节点25 }26 else 27 {28 break;29 }30 }31 // 把祖父节点放到祖孙节点那里32 array[i] = temp;33}34
35void HeapSort(int* array, int length) {36 int i;37
38 // 先处理内节点,让内节点都是该族的最大值39 for(i = (length - 1) / 2; i >= 0; i--) 40 {41 Sift(array, i, length - 1);42 }43
44 // 再从上到下,处理所有节点45 for(i = length - 1; i >= 1; i--) 46 {47 // 根节点是最大的值,和最后一个值交换48 int temp = array[i];49 array[i] = array[0];50 array[0] = temp;51
52 // 最后一个值已经处理了,所以 i-153 Sift(array, 0, i - 1);54 }55}56
57
58int main() {59 int array[100];60 int length;61 int i;62
63 scanf("%d", &length);64 for(i = 0; i < length; i++) 65 {66 scanf("%d", &array[i]);67 }68
69 for(i = 0; i < length; i++) 70 {71 printf("->%d\n", array[i]);72 }73
74 HeapSort(array, length);75
76
77 for(i = 0; i < length; i++) 78 {79 printf("--->%d\n", array[i]);80 }81
82
83}84
85/*86test case 01:8710889 3 1 2 5 4 6 8 7 089*/运行结果
复杂度
| 平均时间复杂度 | |
|---|---|
| 最坏时间复杂度 | |
| 最优时间复杂度 | |
| 空间复杂度 | 总共 |
| 最佳解 | 不是 |
堆排序的稳定性